The Gamma function

A diagram containing operators of various orders.

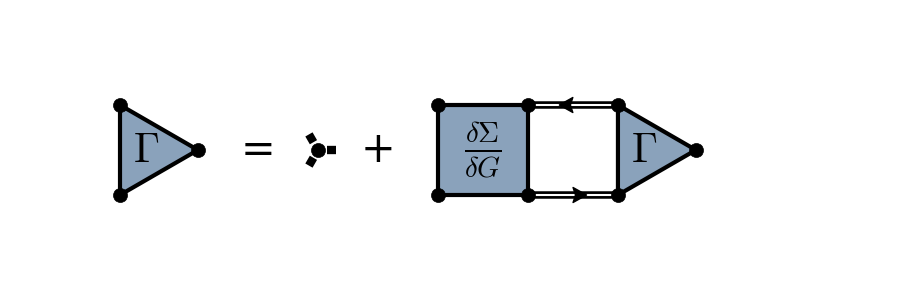
import numpy as np
import matplotlib.pyplot as plt
from feynman import Diagram

# Set up the figure and ax
fig = plt.figure(figsize=(9,3))
ax = fig.add_axes([0,0,1,1], frameon=False)

ax.set_xlim(0, 3)
ax.set_ylim(0, 1)

y0 = sum(ax.get_ylim())/2.

side = 0.3
gammalen = side * np.sqrt(3) / 2
linlen = 0.3
txtpad = 0.2
tail_marker = 'o'

W_style = dict(style = 'double wiggly', nwiggles=2)
v_style = dict(style = 'simple wiggly', nwiggles=2)
G_style = dict(style = 'double',  arrow=True, arrow_param={'width':0.05})

D = Diagram(ax)

# Left hand size
xy = [0.4, y0]
v11 = D.vertex(xy, dy= side/2)
v12 = D.vertex(xy, dy=-side/2)
v13 = D.vertex(xy, dx=gammalen)
gamma0 = D.operator([v11,v12,v13])
gamma0.text("$\Gamma$")

# Symbol
D.text(v13.x + txtpad, y0, "=")

# Create a three-vertex dot.
chunkdist = .03
chunklen = .03
chunkstyle=dict(arrow=False, linewidth=6.)
v20 = D.vertex([v13.x + 2 * txtpad, y0])
v210 = D.vertex(v20.xy, angle=0.,   radius=chunkdist, marker='')
v220 = D.vertex(v20.xy, angle=1./3, radius=chunkdist, marker='')
v230 = D.vertex(v20.xy, angle=2./3, radius=chunkdist, marker='')
v21  = D.vertex(v20.xy, angle=0.,   radius=chunkdist+chunklen, marker='')
v22  = D.vertex(v20.xy, angle=1./3, radius=chunkdist+chunklen, marker='')
v23  = D.vertex(v20.xy, angle=2./3, radius=chunkdist+chunklen, marker='')
D.line(v210, v21, **chunkstyle)
D.line(v220, v22, **chunkstyle)
D.line(v230, v23, **chunkstyle)

# Symbol
D.text(v20.x + txtpad, y0, "+")

# Second term
xy = [v20.x + 2 * txtpad, y0]
v31 = D.vertex(xy, dy= side/2)
v32 = D.vertex(xy, dy=-side/2)
v33 = D.vertex(xy, dy= side/2, dx=side)
v34 = D.vertex(xy, dy=-side/2, dx=side)
K = D.operator([v31,v32,v34,v33])
K.text("$\\frac{\delta \Sigma}{\delta G}$")

v41 = D.vertex(v33.xy, dx=linlen)
v42 = D.vertex(v34.xy, dx=linlen)
v43 = D.vertex((v41.xy+v42.xy)/2, dx=gammalen)

G1 = D.line(v41, v33, **G_style)
G2 = D.line(v34, v42, **G_style)

gamma1 = D.operator([v41,v42,v43])
gamma1.text("$\Gamma$")


# Plot and show
D.plot()
plt.show()

Total running time of the script: ( 0 minutes 0.078 seconds)